Bài 6 trang 45 SGK Hình học 12 Nâng cao

LG a

Tìm tập hợp các mặt cầu tiếp xúc với ba cạnh của một tam giác cho trước.

Lời giải chi tiết:

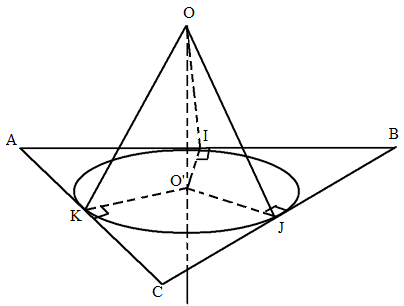
Mặt cầu tâm \(O\) tiếp xúc với ba cạnh \(AB, BC, CA\) của tam giác \(ABC\) lần lượt tại các điểm \(I, J, K\) khi và chỉ khi \(OI \bot AB\,\,,\,\,OJ \bot BC\,\,,\,\,OK \bot CA\), \(OI = OJ = OK\,\, \in \left( * \right)\)

Gọi \(O’\) là hình chiếu vuông góc của \(O\) trên mp \((ABC)\) thì các điều kiện (*) tương đương với \(O'I \bot AB\,\,,\,\,O'J \bot BC\,\,,\,\,O'K \bot CA,\) \(O'I = O'J = O'K\) hay \(O’\) là tâm đường tròn nội tiếp tam giác \(ABC\).

Từ đó suy ra tập hợp các điểm \(O\) là trục của đường tròn nội tiếp tam giác \(ABC\).

LG b

Chứng minh rằng nếu có mặt cầu tiếp xúc với sáu cạnh của hình tứ diện \(ABCD\) thì \(AB + CD = AC + BD = AD + BC\)

Lời giải chi tiết:

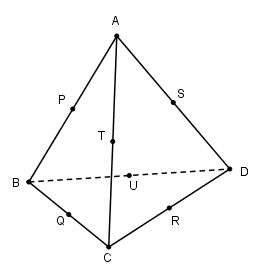
Giả sử mặt cầu \((S)\) nội tiếp với các cạnh \(AB, BC, CD, DA, AC, BD\) lần lượt tại \(P, Q, R, S, T, U\).

Ta cần chứng minh: \(AB + CD = AC + BD = AD + BC\)

Theo tính chất của tiếp tuyến ta có:

\(\eqalign{
& AB + CD = AP + PB + CR + RD \cr 
& = AT + BU + CT + DU \cr 
& = \left( {AT + TC} \right) + \left( {BU + UD} \right) \cr &= AC + BD \cr} \)

Vậy \(AB + CD = AC + BD\)

Chứng minh tương tự \(AC + BD = AD + BC\)

Vậy \(AB + CD = AC + BD = AD + BC\).