Bài 5 trang 111 SGK Toán 9 tập 2

Đề bài

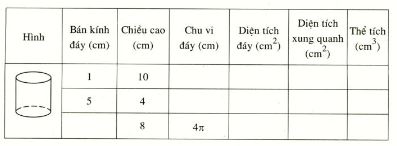
Điền đầy đủ kết quả vào những ô trống của bảng sau:

Lời giải chi tiết

+ Khi \(r = 1cm;h = 10cm\) thì hình trụ có

- Chu vi đáy \(C = 2\pi r = 2\pi \left( {cm} \right)\)

- Diện tích đáy là \(S = \pi {r^2} = \pi {.1^2} = \pi \left( {c{m^2}} \right)\)

- Diện tích xung quanh là \({S_{xq}} = 2\pi rh = 2\pi .1.10 = 20\pi \left( {c{m^2}} \right)\)

- Thể tích là \(V = \pi {r^2}h = \pi {.1^2}.10 = 10\pi \left( {c{m^3}} \right)\)

+ Khi \(r = 5cm;h = 4cm\) thì hình trụ có 

- Chu vi đáy \(C = 2\pi r = 2\pi .5 = 10\pi \left( {cm} \right)\)

- Diện tích đáy là \(S = \pi {r^2} = \pi {.5^2} = 25\pi \left( {c{m^2}} \right)\)

- Diện tích xung quanh là \[{S_{xq}} = 2\pi rh = 2\pi .5.4 = 40\pi \left( {c{m^2}} \right)\]

- Thể tích là \(V = \pi {r^2}h = \pi {.5^2}.4 = 100\pi \left( {c{m^3}} \right)\)

+ Khi \(h = 8cm\) và chi vi đáy \(C = 4\pi \) thì hình trụ có

- Bán kính đáy \(r = \dfrac{C}{{2\pi }} = \dfrac{{4\pi }}{{2\pi }} = 2\left( {cm} \right)\)

- Diện tích đáy là \(S = \pi {r^2} = \pi {.2^2} = 4\pi \left( {c{m^2}} \right)\)

- Diện tích xung quanh là \({S_{xq}} = 2\pi rh = 2\pi .2.8 = 32\pi \left( {c{m^2}} \right)\)

- Thể tích là \(V = \pi {r^2}h = \pi {.2^2}.8 = 32\pi \left( {c{m^3}} \right)\)

Vậy ta có bảng sau: