Bài 45 trang 124 SGK Toán 8 tập 2
Giải bài 45 trang 124 SGK Toán 8 tập 2. Tính thể tích của mỗi hình chop đều dưới đây
Đề bài
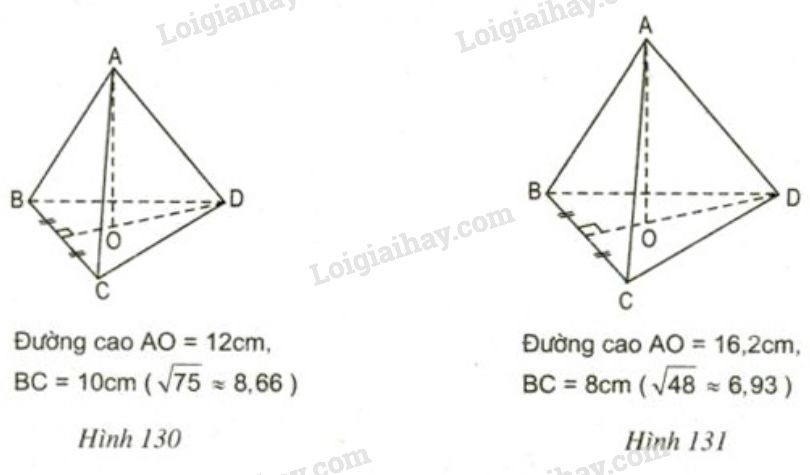
Tính thể tích của mỗi hình chóp đều dưới đây (h130, h131).
Phương pháp giải - Xem chi tiết
Tính thể tích hình chóp theo công thức: \(V = \dfrac{1}{3} .S.h\), trong đó \(S\) là diện tích đáy, \(h\) là chiều cao.
Lời giải chi tiết
+) Hình 130
Đáy của hình chóp là tam giác đều cạnh bằng \(10cm\) như hình vẽ:
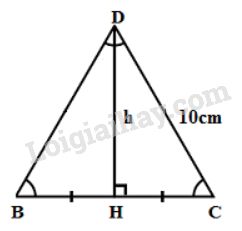
Đường cao của tam giác đều \(BDC\) là:
\(h= HD =\sqrt{DC^{2} - HC^{2}} \) \(= \sqrt{DC^{2} -{\left( {\dfrac{{BC}}{2}} \right)^2}} \)
\(= \sqrt{10^{2} - 5^{2}} = \sqrt{75}\approx 8,66 (cm) \)
Diện tích đáy của hình chóp đều là:
\(S= \dfrac{1}{2}. BC. h = \dfrac{1}{2}. 10. 8,66 =43,3 \) \((cm^2) \)
Thể tích hình chóp đều là:
\( V= \dfrac{1}{3} .S.AO = \dfrac{1}{3} .43,3 .12 =173,2 \) \((cm^3)\)
+) Hình 131:
Đáy của hình chóp là tam giác đều cạnh bằng \(8cm\) như hình vẽ:
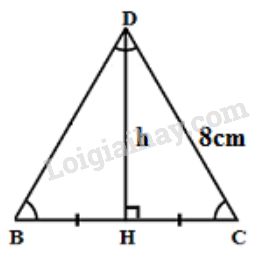
Đường cao của tam giác đều \(BDC\) là:
\(h= HD =\sqrt{DC^{2} - HC^{2}} \) \(= \sqrt{DC^{2} - {\left( {\dfrac{{BC}}{2}} \right)^2}} \)
\(= \sqrt{8^{2} - 4^{2}} = \sqrt{48}\approx 6,93 (cm) \)
Diện tích đáy của hình chóp đều là:
\(S= \dfrac{1}{2}. BC. h = \dfrac{1}{2}. 8. 6,93 =27,72 \) \((cm^2) \)
Thể tích hình chóp đều là:
\( V= \dfrac{1}{3} .S.AO = \dfrac{1}{3} .27,72 .16,2 \)\(\,\approx 149,69\) \( (cm^3)\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 45 trang 124 SGK Toán 8 tập 2 timdapan.com"







