Bài 38 trang 91 SGK Toán 6 tập 2
Giải bài 38 trang 91 SGK Toán 6 tập 2. Trong hình 48, ta có hai đường tròn(O;2cm) và (A;2cm) cắt nhau tại C,D. Điểm A nằm trên đường tròn tâm O.
Đề bài
Trong hình 48, ta có hai đường tròn \((O;2cm)\) và \((A;2cm)\) cắt nhau tại \(C, D.\) Điểm \(A\) nằm trên đường tròn tâm \(O.\)
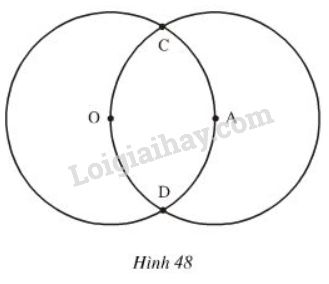
a) Vẽ đường tròn tâm \(C,\) bán kính \(2cm.\)
b) Vì sao đường tròn \((C;2cm)\) đi qua \(O,A?\)
Phương pháp giải - Xem chi tiết
Đường tròn tâm O, bán kính \(R\) là hình gồm các điểm cách \(O\) một khoảng bằng \(R,\) kí hiệu \((O;R).\)
Ta dùng compa để vẽ đường tròn.
Lời giải chi tiết
a) Lấy C làm tâm, mở khẩu độ compa bằng 2cm. Vẽ đường tròn tâm C bán kính 2cm
Xem hình bên:
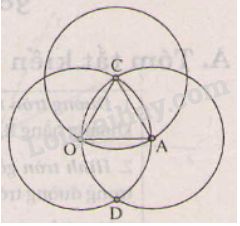
b)
Vì hai đường tròn \((O; 2cm)\) và \((A; 2cm)\) cắt nhau tại \(C\) nên:
- Điểm \(C\) thuộc \((O; 2cm) ⇒ OC = 2cm\) do đó \(O\) thuộc \((C; 2cm)\)
- Điểm \(C\) thuộc \((A; 2cm) ⇒ AC = 2cm\) do đó \(A\) thuộc \((C; 2cm)\)
Vậy đường tròn \((C; 2cm)\) đi qua hai điểm \(O\) và \(A.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 38 trang 91 SGK Toán 6 tập 2 timdapan.com"







