Bài 38 trang 41 SGK Toán 7 tập 2

Cho các đa thức:

          \(A = {x^2}-2y + xy + 1\)

           \(B = {x^2} + y - {x^2}{y^2} - 1\).

Tìm đa thức \(C\) sao cho:

LG a

\(C = A + B\)

Phương pháp giải:

Đa thức \(C\) là tổng của hai đa thức \(A\) và \(B\).

Giải chi tiết:

Ta có: \(A = {x^2}-2y + xy + 1\)

          \(B = {x^2} + y - {x^2}{y^2} - 1\).

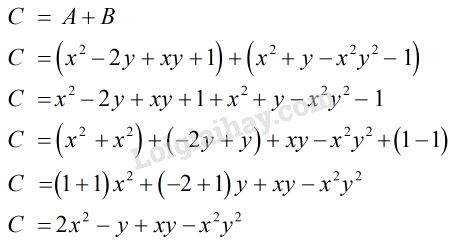
Vậy đa thức \(C = 2{x^2}-y + xy - {x^2}{y^2}\)

LG b

\(C + A = B\)

Phương pháp giải:

\(C\) có vai trò là số hạng chưa biết. Muốn tìm số hạng chưa biết ta lấy tổng trừ đi số hạng đã biết.

Tức là đa thức \(C\) là hiệu của hai đa thức \(B\) và \(A\). 

Giải chi tiết:

Vậy đa thức \(C =  - {x^2}{y^2} - xy + 3y - 2\)