Bài 38 trang 129 SGK Toán 9 tập 2
Giải bài 38 trang 129 SGK Toán 9 tập 2 . Hãy tính thể tích , diện tích bề mặt một chi tiết máy theo kích thước đã cho trên hình 114.
Đề bài
Hãy tính thể tích , diện tích bề mặt một chi tiết máy theo kích thước đã cho trên hình 114.
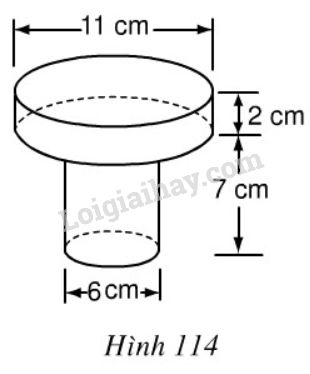
Phương pháp giải - Xem chi tiết
+) Diện tích xung quanh của hình trụ: \(S_{xq}=2\pi rh.\)
+) Diện tích toàn phần của hình trụ: \(S_{tp}=2 \pi rh +2 \pi r^2.\)
+) Thể tích hình trụ là: \(V=\pi r^2h.\)
Lời giải chi tiết
* Ta có: Thể tích phần cần tính là tổng thể tích của hai hình trụ có đường kính là \(11cm\) và chiều cao là \(2cm\).
\(\displaystyle {V_1} = \pi {R^2}{h_1} = \pi {\left( {{{11} \over 2}} \right)^2}.2 = 60,5\pi \left( {c{m^3}} \right)\)
Thể tích hình trụ có đường kính đáy là \(6cm\), chiều cao là \(7cm\)
\(\displaystyle {V_2} = \pi {R^2}{h_2} = \pi {\left( {{6 \over 2}} \right)^2}.7 = 63\pi \left( {c{m^3}} \right)\)
Vậy thể tích của chi tiết máy cần tính là:
\(V = {V_1} + {V_2} = 60,5\pi + 63\pi = 123,5\pi (c{m^3})\)
* Tương tự, theo đề bài diện tích bề mặt của chi tiết máy bằng tổng diện tích xung quanh của hai chi tiết máy với diện tích 2 hình tròn đáy của hình trụ nằm trên.
Diện tích toàn phần của hình trụ có đường kính đáy \(11 cm\), chiều cao là \(2cm\) và là:
\({S_{tp(1)}} = 2\pi R_1{h_1} + 2\pi {R_1}^2 \)
\(\displaystyle = 2\pi {{11} \over 2}.2 + 2\pi .5,5^2 = 82,5 \pi \left( {c{m^2}} \right)\)
Diện tích xung quanh của hình trụ có đường kính đáy là \(6cm\) và chiều cao là \(7cm\) là:
\(\displaystyle {S_{xq(2)}} = 2\pi R_2 {h_2} = 2\pi {6 \over 2}.7 = 42\pi \left( {c{m^2}} \right)\)
Vậy diện tích bề mặt của chi tiết máy là:
\(S = {S_{tp(1)}} + {\rm{ }}{S_{xq(2)}} = 82,5\pi + 42\pi = 124,5\pi (c{m^2}).\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 38 trang 129 SGK Toán 9 tập 2 timdapan.com"







