Bài 3 trang 16 Tài liệu dạy – học Toán 9 tập 2
Giải bài tập Bạn Lan chuẩn bị bữa điểm tâm gồm đậu phộng với mì xào. Biết rằng cứ mỗi 30 g đậu phộng
Đề bài
Bạn Lan chuẩn bị bữa điểm tâm gồm đậu phộng với mì xào. Biết rằng cứ mỗi 30 g đậu phộng chứa 7 g protein, 30 g mì xào chứa 3 g protein. Để bữa ăn có tổng khối lượng 200 g cung cấp đủ 28 g protein thì bạn Lan cần bao nhiêu gram mỗi loại ?

Phương pháp giải - Xem chi tiết
Gọi khối lượng đậu phộng cần chuẩn bị là \(30x\,\,\left( {gram} \right)\), khối lượng mì xào cần chuẩn bị là \(30y\,\,\left( {gram} \right)\) (\(x,y > 0)\)
Bữa ăn có tổng khối lượng là 200 g nên: …
30x g đậu phộng chứa … protein.
30y gam mì xào chứa … protein.
Bữa ăn cung cấp cung cấp đủ 28 g protein nên …
Suy ra hệ phương trình, biểu diễn hai đường thẳng trên mặt phẳng Oxy và xác định giao điểm, từ đó suy ra nghiệm của hệ phương trình.
Kết luận :…
Lời giải chi tiết
Gọi khối lượng đậu phộng cần chuẩn bị là \(30x\,\,\left( {gram} \right)\), khối lượng mì xào cần chuẩn bị là \(30y\,\,\left( {gram} \right)\) (\(x,y > 0)\)
Bữa ăn có tổng khối lượng là 200 g nên: \(30x + 30y = 200\)
30x g đậu phộng chứa \(7x\,\,\left( g \right)\) protein.
30y gam mì xào chứa \(3y\,\,\left( g \right)\) protein.
Bữa ăn cung cấp cung cấp đủ 28 g protein nên \(7x + 3y = 28\)
Ta có hệ phương trình \(\left\{ \begin{array}{l}30x + 30y = 200\\7x + 3y = 28\end{array} \right.\,\,\left( I \right)\)
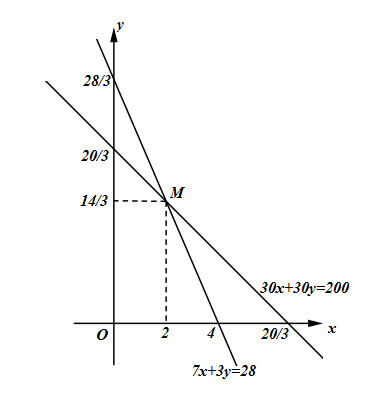
Hai đường thẳng \(30x + 30y = 200\)và \(7x + 3y = 28\) cắt nhau tại điểm \(M\left( {2;\dfrac{{14}}{3}} \right)\) nên \(\left( {x;y} \right) = \left( {2;\dfrac{{14}}{3}} \right)\) là nghiệm của hệ phương trình (I).
Vậy khối lượng đậu phộng cần chuẩn bị là \(60\)g, khối lượng mì xào cần chuẩn bị là 140 g.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 3 trang 16 Tài liệu dạy – học Toán 9 tập 2 timdapan.com"







