Bài 18 trang 59 SGK Hình học 12 Nâng cao
Cho điểm A nằm trong mặt cầu S. Chứng minh rằng các đường thẳng đi qua A tiếp xúc với mặt cầu S luôn nằm trên một mặt nón xác định.
Đề bài
Cho điểm \(A\) nằm ngoài mặt cầu \(S\). Chứng minh rằng các đường thẳng đi qua \(A\) tiếp xúc với mặt cầu \(S\) luôn nằm trên một mặt nón xác định.
Lời giải chi tiết
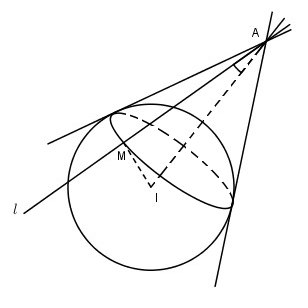
Giả sử \(Al\) là một tiếp tuyến của mặt cầu \(S(I;R)\) với tiếp điểm là \(M\).
Khi đó nếu \(\Delta \) là đường thẳng \(AI\) và \(\alpha \) là góc giữa đường thẳng \(Al\) và \(\Delta \) thì \(\alpha = \widehat {MAI}\).
Ta có: \(\sin \alpha = {{MI} \over {IA}} = {R \over {IA}}\), suy ra góc \(\alpha \) không đổi.
Vậy \(Al\) là đường sinh của mặt nón \((N)\) có đỉnh \(A\) và góc ở đỉnh là \(2\alpha \).
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 18 trang 59 SGK Hình học 12 Nâng cao timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 18 trang 59 SGK Hình học 12 Nâng cao timdapan.com"