Bài 25: Giao thoa ánh sáng
Video bài giảng
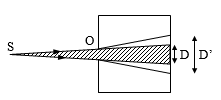
1. Hiện tượng nhiễu xạ ánh sáng
-
Hiện tượng truyền sai lệch so với sự truyền thẳng khi ánh sáng gặp vật cản gọi là hiện tượng nhiễu xạ ánh sáng.
-
Mỗi ánh sáng đơn sắc coi như một sóng có bước sóng xác định.
2. Hiện tượng giao thoa ánh sáng
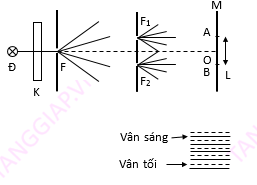
a. Thí nghiệm Y-âng về giao thoa ánh sáng
-
Ánh sáng từ bóng đèn Đ → trên M trông thấy một hệ vân có nhiều màu.
-
Đặt kính màu K (đỏ…) → trên M chỉ có một màu đỏ và có dạng những vạch sáng đỏ và tối xen kẽ, song song và cách đều nhau.
-
Giải thích:
-
Hai sóng kết hợp phát đi từ \(F_1\) , \(F_2\) gặp nhau trên M đã giao thoa với nhau:
-
Hai sóng gặp nhau tăng cường lẫn nhau → vân sáng.
-
Hai sóng gặp nhau triệt tiêu lẫn nhau → vân tối.
-
b. Vị trí vân sáng
.png)
-
Với a = \(S_1S_2\); D khoảng cách từ mặt phẳng chứa \(S_1S_2\)
→ Màu \(d_1d_2\) là khoảng cách từ M đến \(S_1S_2\)
-
Gọi \(\lambda\): là bước sóng của ánh sáng đơn sắc.
\(\Rightarrow d_2-d_1=\frac{a.x}{D}\)
-
Vị trí vân sáng (cực đại): \(d_2-d_1=k.\lambda\)
\(\begin{array}{l}
\Rightarrow \frac{{a.{x_s}}}{D} = k.\lambda \\
\Rightarrow {x_s} = k.\frac{{\lambda .D}}{a},k = 0, \pm 1, \pm 2
\end{array}\)
-
Vị trí các vân tối (cực tiểu): \(d_2-d_1= (k'+\frac{1}{2}).\lambda\)
\(\begin{array}{l}
\Rightarrow \frac{{a.{x_t}}}{D} = (k' + \frac{1}{2})\lambda \\
\Rightarrow {x_t} = (k' + \frac{1}{2}).\frac{{\lambda .D}}{a}.\\
k' \in Z
\end{array}\)
c. Khoảng vân
-
Định nghĩa: Khoảng vân i là khỏang cách giữa hai vân sáng hoặc hai vân tối liên tiếp nhau.
-
Công thức tính khoảng vân:
\(i=\frac{\lambda .D}{a}\)
-
Tại O là vân sáng bậc 0 của mọi bức xạ: vân chính giữa hay vân trung tâm, hay vân số 0.
d. Ứng dụng:
-
Đo bước sóng ánh sáng.
-
Nếu biết i, a, D sẽ suy ra được :
Từ \(i=\frac{\lambda .D}{a}\Rightarrow \lambda =\frac{a.i}{D}\)
3. Bước sóng và màu sắc
-
Mỗi bức xạ đơn sắc ứng với một bước sóng trong chân không xác định.
-
Mọi ánh sáng đơn sắc mà ta nhìn thấy có: λ = (380→ 760) nm.
-
Ánh sáng trắng của Mặt Trời là hỗn hợp của vô số ánh sáng đơn sắc có bước sóng biến thiên liên tục từ 0 đến ∞.
Bài 1:
Trong thí nghiệm Y - âng về giao thoa ánh sáng, các khe \(S_1\) ,\(S_1\) cách nhau 1mm được chiếu sáng bởi ánh sáng đơn sắc có bước sóng λ = 0,76µm. Biết khoảng cách từ mặt phẳng hai khe \(S_1\) ,\(S_1\) đến màn là 3m. Hỏi tại vị trí cách vân sáng trung tâm 4,56mm là vân sáng thứ mấy?
Hướng dẫn giải:
Khoảng vân:
\(i=\frac{\lambda D}{a}=2,28.10^{-3}m\)
Vị trí vân tối được xác định theo biểu thức:
\(x_t=ki\rightarrow k=\frac{x_t}{i}=2\)
Ứng với k=2 là vân sáng bậc 2.
Bài 2:
Trong thí nghiệm Y - âng về giao thoa ánh sáng, các khe \(S_1\) ,\(S_2\) cách nhau 1mm được chiếu sáng bởi ánh sáng đơn sắc có bước sóng λ = 0,5µm. Biết khoảng cách từ mặt phẳng hai khe \(S_1\) , \(S_2\) đến màn là 3m. Hỏi tại vị trí cách vân sáng trung tâm 5,25mm là vân tối thứ mấy?
Hướng dẫn giải:
Khoảng vân:
\(i=\frac{\lambda D}{a}=1,5.10^{-3}m\)
Vị trí vân tối được xác định theo biểu thức:
\(x_t=(k+\frac{1}{2})i\rightarrow k=\frac{x_t}{i}-\frac{1}{2}=3\)
Ứng với k=3 là vân tối thứ 4.
Bài 3:
Trong thí nghiệm giao thoa ánh sáng với khe Y - âng, người ta chiếu sáng 2 khe bằng ánh sáng đơn sắc có bước sóng λ = 0,5 µm, khoảng cách giữa 2 khe là 2 mm. Khoảng cách từ 2 khe tới màn là 1m. Xác định khoảng cách giữa vân sáng bậc 4 và vân tối thứ 4 ở cùng một phía so với vân trung tâm?
Hướng dẫn giải:
Khoảng vân: \(i=\frac{\lambda D}{a}=2,5.10^{-4}m\)
Khoảng cách từ vân trung tâm tới vân sáng bậc 4 (k=4): x=4i
Khoảng cách từ vân trung tâm tới vân tối thứ 4 (k=3): x=3,5i
Khoảng cách giữa vân sáng bậc 4 và vân tối thứ 4 ở cùng một phía so với vân trung tâm là :
x=4i-3,5i=1,25.\(10^{-4}m\) = 0,125mm
Bài 4:
Trong thí nghiệm của Young về giao thoa ánh sáng, hai khe S1 và S2 được chiếu bằng ánh sáng đơn sắc có bước sóng l = 0,5 mm. Khoảng cách giữa hai khe là 0,8 mm. Người ta đo được khoảng cách giữa 5 vân sáng liên tiếp trên màn là 4 mm. Tính khoảng cách từ hai khe đến màn và cho biết tại 2 điểm C và E trên màn, cùng phía với nhau so với vân sáng trung tâm và cách vân sáng trung tâm lần lượt là :
Hướng dẫn giải:
Ta có:
\(i=\frac{L}{5-1}=1mm; D=\frac{ai}{\lambda }=1,6m\)
\(\frac{x_C}{i}\) = 2,5 nên tại C ta có vân tối;
\(\frac{x_E}{i}\) = 15 nên tại N ta có vân sáng;
→ Từ C đến E có 13 vân sáng kể cả vân sáng bậc 15 tại E.
1. Hiện tượng nhiễu xạ ánh sáng

-
Hiện tượng truyền sai lệch so với sự truyền thẳng khi ánh sáng gặp vật cản gọi là hiện tượng nhiễu xạ ánh sáng.
-
Mỗi ánh sáng đơn sắc coi như một sóng có bước sóng xác định.
2. Hiện tượng giao thoa ánh sáng
a. Thí nghiệm Y-âng về giao thoa ánh sáng

-
Ánh sáng từ bóng đèn Đ → trên M trông thấy một hệ vân có nhiều màu.
-
Đặt kính màu K (đỏ…) → trên M chỉ có một màu đỏ và có dạng những vạch sáng đỏ và tối xen kẽ, song song và cách đều nhau.
-
Giải thích:
-
Hai sóng kết hợp phát đi từ \(F_1\) , \(F_2\) gặp nhau trên M đã giao thoa với nhau:
-
Hai sóng gặp nhau tăng cường lẫn nhau → vân sáng.
-
Hai sóng gặp nhau triệt tiêu lẫn nhau → vân tối.
-
b. Vị trí vân sáng
.png)
-
Với a = \(S_1S_2\); D khoảng cách từ mặt phẳng chứa \(S_1S_2\)
→ Màu \(d_1d_2\) là khoảng cách từ M đến \(S_1S_2\)
-
Gọi \(\lambda\): là bước sóng của ánh sáng đơn sắc.
\(\Rightarrow d_2-d_1=\frac{a.x}{D}\)
-
Vị trí vân sáng (cực đại): \(d_2-d_1=k.\lambda\)
\(\begin{array}{l}
\Rightarrow \frac{{a.{x_s}}}{D} = k.\lambda \\
\Rightarrow {x_s} = k.\frac{{\lambda .D}}{a},k = 0, \pm 1, \pm 2
\end{array}\)
-
Vị trí các vân tối (cực tiểu): \(d_2-d_1= (k'+\frac{1}{2}).\lambda\)
\(\begin{array}{l}
\Rightarrow \frac{{a.{x_t}}}{D} = (k' + \frac{1}{2})\lambda \\
\Rightarrow {x_t} = (k' + \frac{1}{2}).\frac{{\lambda .D}}{a}.\\
k' \in Z
\end{array}\)
c. Khoảng vân
-
Định nghĩa: Khoảng vân i là khỏang cách giữa hai vân sáng hoặc hai vân tối liên tiếp nhau.
-
Công thức tính khoảng vân:
\(i=\frac{\lambda .D}{a}\)
-
Tại O là vân sáng bậc 0 của mọi bức xạ: vân chính giữa hay vân trung tâm, hay vân số 0.
d. Ứng dụng:
-
Đo bước sóng ánh sáng.
-
Nếu biết i, a, D sẽ suy ra được :
Từ \(i=\frac{\lambda .D}{a}\Rightarrow \lambda =\frac{a.i}{D}\)
3. Bước sóng và màu sắc
-
Mỗi bức xạ đơn sắc ứng với một bước sóng trong chân không xác định.
-
Mọi ánh sáng đơn sắc mà ta nhìn thấy có: λ = (380→ 760) nm.
-
Ánh sáng trắng của Mặt Trời là hỗn hợp của vô số ánh sáng đơn sắc có bước sóng biến thiên liên tục từ 0 đến ∞.
Bài 1:
Trong thí nghiệm Y - âng về giao thoa ánh sáng, các khe \(S_1\) ,\(S_1\) cách nhau 1mm được chiếu sáng bởi ánh sáng đơn sắc có bước sóng λ = 0,76µm. Biết khoảng cách từ mặt phẳng hai khe \(S_1\) ,\(S_1\) đến màn là 3m. Hỏi tại vị trí cách vân sáng trung tâm 4,56mm là vân sáng thứ mấy?
Hướng dẫn giải:
Khoảng vân:
\(i=\frac{\lambda D}{a}=2,28.10^{-3}m\)
Vị trí vân tối được xác định theo biểu thức:
\(x_t=ki\rightarrow k=\frac{x_t}{i}=2\)
Ứng với k=2 là vân sáng bậc 2.
Bài 2:
Trong thí nghiệm Y - âng về giao thoa ánh sáng, các khe \(S_1\) ,\(S_2\) cách nhau 1mm được chiếu sáng bởi ánh sáng đơn sắc có bước sóng λ = 0,5µm. Biết khoảng cách từ mặt phẳng hai khe \(S_1\) , \(S_2\) đến màn là 3m. Hỏi tại vị trí cách vân sáng trung tâm 5,25mm là vân tối thứ mấy?
Hướng dẫn giải:
Khoảng vân:
\(i=\frac{\lambda D}{a}=1,5.10^{-3}m\)
Vị trí vân tối được xác định theo biểu thức:
\(x_t=(k+\frac{1}{2})i\rightarrow k=\frac{x_t}{i}-\frac{1}{2}=3\)
Ứng với k=3 là vân tối thứ 4.
Bài 3:
Trong thí nghiệm giao thoa ánh sáng với khe Y - âng, người ta chiếu sáng 2 khe bằng ánh sáng đơn sắc có bước sóng λ = 0,5 µm, khoảng cách giữa 2 khe là 2 mm. Khoảng cách từ 2 khe tới màn là 1m. Xác định khoảng cách giữa vân sáng bậc 4 và vân tối thứ 4 ở cùng một phía so với vân trung tâm?
Hướng dẫn giải:
Khoảng vân: \(i=\frac{\lambda D}{a}=2,5.10^{-4}m\)
Khoảng cách từ vân trung tâm tới vân sáng bậc 4 (k=4): x=4i
Khoảng cách từ vân trung tâm tới vân tối thứ 4 (k=3): x=3,5i
Khoảng cách giữa vân sáng bậc 4 và vân tối thứ 4 ở cùng một phía so với vân trung tâm là :
x=4i-3,5i=1,25.\(10^{-4}m\) = 0,125mm
Bài 4:
Trong thí nghiệm của Young về giao thoa ánh sáng, hai khe S1 và S2 được chiếu bằng ánh sáng đơn sắc có bước sóng l = 0,5 mm. Khoảng cách giữa hai khe là 0,8 mm. Người ta đo được khoảng cách giữa 5 vân sáng liên tiếp trên màn là 4 mm. Tính khoảng cách từ hai khe đến màn và cho biết tại 2 điểm C và E trên màn, cùng phía với nhau so với vân sáng trung tâm và cách vân sáng trung tâm lần lượt là :
Hướng dẫn giải:
Ta có:
\(i=\frac{L}{5-1}=1mm; D=\frac{ai}{\lambda }=1,6m\)
\(\frac{x_C}{i}\) = 2,5 nên tại C ta có vân tối;
\(\frac{x_E}{i}\) = 15 nên tại N ta có vân sáng;
→ Từ C đến E có 13 vân sáng kể cả vân sáng bậc 15 tại E.