Bài 5: Điện thế và hiệu điện thế
1. Điện thế
1.1. Khái niệm điện thế
-
Điện thế tại một điểm trong điện trường đặc trưng cho điện trường về phương diện tạo ra thế năng của điện tích.
1.2. Định nghĩa
-
Điện thế tại một điểm M trong điện trường là đại lượng đặc trưng cho điện trường về phương diện tạo ra thế năng khi đặt tại đó một điện tích q. Nó được xác định bằng thương số của công của lực điện tác dụng lên điện tích q khi q di chuyển từ M ra xa vô cực và độ lớn của q
-
Công thức: \({V_M} = \frac{{{A_{M\infty }}}}{q}\)
-
Đơn vị điện thế là vôn (V).
\(1V = \frac{{1J}}{{1C}}\)
1.3. Đặc điểm của điện thế
-
Điện thế là đại lượng đại số. Thường chọn điện thế ở mặt đất hoặc một điểm ở vô cực làm mốc (bằng 0).
-
Với q > 0, nếu \({A_{M\infty }} > 0\) thì \({V_M} > {\rm{ }}0\)
-
Nếu \({A_{M\infty }} < 0\) thì \({V_M} < {\rm{ }}0\).
2. Hiệu điện thế
2.1. Định nghĩa
-
Hiệu điện thế giữa hai điểm M, N trong điện trường là đại lượng đặc trưng cho khả năng sinh công của điện trường trong sự di chuyển của một điện tích từ M đến N. Nó được xác định bằng thương số giữa công của lực điện tác dụng lên điện tích q trong sự di chuyển của q từ M đến N và độ lớn của q.
\({U_{MN}} = {\rm{ }}{V_M}-{V_N} = \frac{{{A_{MN}}}}{q}\)
-
Đơn vị hiệu điện thế là V (Vôn)
2.2. Đo hiệu điện thế
-
Đo hiệu điện thế tĩnh điện bằng tĩnh điện kế.
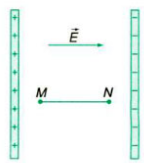
2.3. Hệ thức liên hệ giữa hiệu điện thế và cường độ điện trường
Xét 2 điểm M, N trên một đường sức điện của một điện trường đều
-
Hiệu điện thế:
\({U_{MN}} = \frac{{{A_{MN}}}}{q} = Ed\)
-
Cường độ điện trường:
\(E = \frac{{{U_{MN}}}}{d} = \frac{U}{d}\)
Công thức này đúng cho trường hợp điện trường không đều, nếu trong khoảng d rất nhỏ dọc theo đường sức điện, cường độ điện trường thay đổi không đáng kể.
-
Chú ý:
-
Điện thế, hiệu điện thế là một đại lượng vô hướng có giá trị dương hoặc âm;
-
Hiệu điện thế giữa hai điểm M, N trong điện trường có giá trị xác định còn điện thế tại một điểm trong điện trường có giá trị phụ thuộc vào vị trí ta chọn làm gốc điện thế.
-
Trong điện trường, véctơ cường độ điện trường có hướng từ nơi có điện thế cao sang nơi có điện thế thấp;
-
Bài 1:
Khi một điện tích q = -2C di chuyển từ điểm M đến điểm N trong điện trường thì lực điện sinh công -6 J. Hỏi hiệu điện thế \(U_{{MN}}\) có giá trị nào sau đây ?
Hướng dẫn giải:
-
Áp dụng công thức tính hiệu điện thế của một điện tích q di chuyển từ điểm M đến điểm N trong điện trường.
-
Ta có: \({U_{MN}} = \frac{{{A_{MN}}}}{q} = - \frac{6}{{ - 2}} = 3V\)
Bài 2:
Cho ABC là một tam giác vuông góc tại A được đặt trong điện trường đều \(\vec E\) .
Biết \(\alpha = \widehat {ABC} = {60^0},BC = 6cm,\,{U_{BC}} = 120V\)
a). Tìm \({U_{AC,}}\,\,{U_{BA}}\) và độ lớn \(\vec E\) .
b). Đặt thêm ở C một điện tích \(q{\rm{ }} = {\rm{ }}{9.10^{ - 10}}C\) .Tính cường độ điện trường tổng hợp tại A.
Hướng dẫn giải:
a. là \(\frac{1}{2}\) tam giác đều, vậy nếu BC = 6cm.
Suy ra: BA = 3cm và \(AC = \frac{{6\sqrt 3 }}{2} = 3\sqrt 3 \)
\({U_{BA}} = {\rm{ }}{U_{BC}} = {\rm{ }}120V,{\rm{ }}{U_{AC}} = {\rm{ }}0\)
\(E = \frac{U}{d} = \frac{{{U_{BA}}}}{{BA}} = 4000V/m\) .
b.
\(\begin{array}{l}
\overrightarrow {{E_A}} = \overrightarrow {{E_C}} + \vec E\\
\Rightarrow {E_A} = \sqrt {{E_C}^2 + {E^2}} = 5000V/m
\end{array}\)
1. Điện thế
1.1. Khái niệm điện thế
-
Điện thế tại một điểm trong điện trường đặc trưng cho điện trường về phương diện tạo ra thế năng của điện tích.
1.2. Định nghĩa
-
Điện thế tại một điểm M trong điện trường là đại lượng đặc trưng cho điện trường về phương diện tạo ra thế năng khi đặt tại đó một điện tích q. Nó được xác định bằng thương số của công của lực điện tác dụng lên điện tích q khi q di chuyển từ M ra xa vô cực và độ lớn của q
-
Công thức: \({V_M} = \frac{{{A_{M\infty }}}}{q}\)
-
Đơn vị điện thế là vôn (V).
\(1V = \frac{{1J}}{{1C}}\)
1.3. Đặc điểm của điện thế
-
Điện thế là đại lượng đại số. Thường chọn điện thế ở mặt đất hoặc một điểm ở vô cực làm mốc (bằng 0).
-
Với q > 0, nếu \({A_{M\infty }} > 0\) thì \({V_M} > {\rm{ }}0\)
-
Nếu \({A_{M\infty }} < 0\) thì \({V_M} < {\rm{ }}0\).
2. Hiệu điện thế
2.1. Định nghĩa
-
Hiệu điện thế giữa hai điểm M, N trong điện trường là đại lượng đặc trưng cho khả năng sinh công của điện trường trong sự di chuyển của một điện tích từ M đến N. Nó được xác định bằng thương số giữa công của lực điện tác dụng lên điện tích q trong sự di chuyển của q từ M đến N và độ lớn của q.
\({U_{MN}} = {\rm{ }}{V_M}-{V_N} = \frac{{{A_{MN}}}}{q}\)
-
Đơn vị hiệu điện thế là V (Vôn)
2.2. Đo hiệu điện thế
-
Đo hiệu điện thế tĩnh điện bằng tĩnh điện kế.
2.3. Hệ thức liên hệ giữa hiệu điện thế và cường độ điện trường
Xét 2 điểm M, N trên một đường sức điện của một điện trường đều
-
Hiệu điện thế:
\({U_{MN}} = \frac{{{A_{MN}}}}{q} = Ed\)
-
Cường độ điện trường:
\(E = \frac{{{U_{MN}}}}{d} = \frac{U}{d}\)
Công thức này đúng cho trường hợp điện trường không đều, nếu trong khoảng d rất nhỏ dọc theo đường sức điện, cường độ điện trường thay đổi không đáng kể.
-
Chú ý:
-
Điện thế, hiệu điện thế là một đại lượng vô hướng có giá trị dương hoặc âm;
-
Hiệu điện thế giữa hai điểm M, N trong điện trường có giá trị xác định còn điện thế tại một điểm trong điện trường có giá trị phụ thuộc vào vị trí ta chọn làm gốc điện thế.
-
Trong điện trường, véctơ cường độ điện trường có hướng từ nơi có điện thế cao sang nơi có điện thế thấp;
-
Bài 1:
Khi một điện tích q = -2C di chuyển từ điểm M đến điểm N trong điện trường thì lực điện sinh công -6 J. Hỏi hiệu điện thế \(U_{{MN}}\) có giá trị nào sau đây ?
Hướng dẫn giải:
-
Áp dụng công thức tính hiệu điện thế của một điện tích q di chuyển từ điểm M đến điểm N trong điện trường.
-
Ta có: \({U_{MN}} = \frac{{{A_{MN}}}}{q} = - \frac{6}{{ - 2}} = 3V\)
Bài 2:
Cho ABC là một tam giác vuông góc tại A được đặt trong điện trường đều \(\vec E\) .
Biết \(\alpha = \widehat {ABC} = {60^0},BC = 6cm,\,{U_{BC}} = 120V\)
a). Tìm \({U_{AC,}}\,\,{U_{BA}}\) và độ lớn \(\vec E\) .
b). Đặt thêm ở C một điện tích \(q{\rm{ }} = {\rm{ }}{9.10^{ - 10}}C\) .Tính cường độ điện trường tổng hợp tại A.
Hướng dẫn giải:
a. là \(\frac{1}{2}\) tam giác đều, vậy nếu BC = 6cm.
Suy ra: BA = 3cm và \(AC = \frac{{6\sqrt 3 }}{2} = 3\sqrt 3 \)
\({U_{BA}} = {\rm{ }}{U_{BC}} = {\rm{ }}120V,{\rm{ }}{U_{AC}} = {\rm{ }}0\)
\(E = \frac{U}{d} = \frac{{{U_{BA}}}}{{BA}} = 4000V/m\) .
b.
\(\begin{array}{l}
\overrightarrow {{E_A}} = \overrightarrow {{E_C}} + \vec E\\
\Rightarrow {E_A} = \sqrt {{E_C}^2 + {E^2}} = 5000V/m
\end{array}\)
.PNG)