Giải bài 53 trang 117 sách bài tập toán 11 - Cánh diều
Cho hình chóp (S.ABCD) có đáy là hình bình hành. Trên cạnh (SA) lấy điểm (M)
Đề bài
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Trên cạnh \(SA\) lấy điểm \(M\) sao cho \(MA = 2MS\). Mặt phẳng \(\left( {CDM} \right)\) cắt \(SB\) tại \(N\). Tỉ số \(\frac{{SN}}{{SB}}\) bằng:
A. \(\frac{1}{2}\)
B. \(\frac{1}{3}\)
C. \(\frac{2}{3}\)
D. \(\frac{3}{4}\)
Phương pháp giải - Xem chi tiết
Chứng minh rằng \(MN\) là giao tuyến của hai mặt phẳng \(\left( {CDM} \right)\) và \(\left( {SAB} \right)\), từ đó suy ra \(MN\parallel AB\) và tính tỉ số \(\frac{{SN}}{{SB}}\).
Lời giải chi tiết
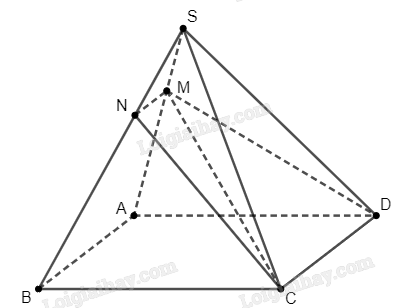
Ta thấy rằng \(M \in \left( {CDM} \right) \cap \left( {SAB} \right)\) và \(N\) là giao điểm của \(\left( {CDM} \right)\) và \(SB\). Do \(SB \subset \left( {SAB} \right)\) nên \(N\) là điểm chung của hai mặt phẳng \(\left( {CDM} \right)\) và \(\left( {SAB} \right)\). Từ đó ta suy ra \(MN\) là giao tuyến của hai mặt phẳng \(\left( {CDM} \right)\) và \(\left( {SAB} \right)\).
Nhận xét rằng \(AB\parallel CD\), \(AB \subset \left( {SAB} \right)\), \(CD \subset \left( {CDM} \right)\), \(MN\) là giao tuyến của hai mặt phẳng \(\left( {CDM} \right)\) và \(\left( {SAB} \right)\), ta suy ra \(MN\parallel AB\).
Theo định lí Thales, ta có \(\frac{{SM}}{{SA}} = \frac{{SN}}{{SB}}\). Do \(MA = 2MS \Rightarrow \frac{{SM}}{{SA}} = \frac{1}{3}\).
Như vậy \(\frac{{SN}}{{SB}} = \frac{1}{3}\). Đáp án đúng là B.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 53 trang 117 sách bài tập toán 11 - Cánh diều timdapan.com"







