Giải bài 36 trang 103 sách bài tập toán 11 - Cánh diều
Cho hình chóp \(S.ABCD\) có hai mặt phẳng \(\left( {SAB} \right)\)
Đề bài
Cho hình chóp \(S.ABCD\) có hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAC} \right)\) cùng vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Khi đó mặt phẳng \(\left( {ABCD} \right)\) vuông góc với đường thẳng:
A. \(SA\).
B. \(SB\).
C. \(SC\).
D. \(SD\).
Phương pháp giải - Xem chi tiết
Sử dụng tính chất “Hai mặt phẳng cắt nhau và cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng cũng vuông góc với mặt phẳng thứ ba đó.
Lời giải chi tiết
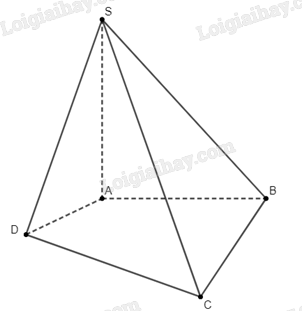
Vì \(\left( {SAB} \right) \bot \left( {ABCD} \right)\), \(\left( {SAC} \right) \bot \left( {ABCD} \right)\), \(SA = \left( {SAB} \right) \cap \left( {SAC} \right)\), nên \(SA \bot \left( {ABCD} \right)\)
Đáp án đúng là A.
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 36 trang 103 sách bài tập toán 11 - Cánh diều timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 36 trang 103 sách bài tập toán 11 - Cánh diều timdapan.com"







