Bài 4 trang 34 SGK Hình học 10 Nâng cao

Cho tam giác \(ABC\).

LG a

Tìm các điểm \(M\) và \(N\) sao cho

\(\overrightarrow {MA}  - \overrightarrow {MB}  + \overrightarrow {MC}  = \overrightarrow 0 \) và \(2\overrightarrow {NA}  + \overrightarrow {NB}  + \overrightarrow {NC}  = \overrightarrow 0 .\)

Giải chi tiết:

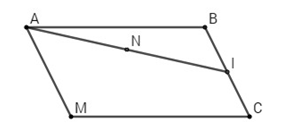
Ta có \(\overrightarrow {MA}  - \overrightarrow {MB}  + \overrightarrow {MC}  = \overrightarrow 0 \, \Leftrightarrow \,\overrightarrow {BA}  + \overrightarrow {MC}  = \overrightarrow 0 \)

\( \Leftrightarrow \,\overrightarrow {CM}  = \overrightarrow {BA} \,.\) Do đó \(ABCM\) là hình bình hành.

Gọi \(I\) là trung điểm của \(BC\), ta có \(\overrightarrow {NB}  + \overrightarrow {NC}  = 2\overrightarrow {NI} \) suy ra \(2\overrightarrow {NA}  + 2\overrightarrow {NI}  = \overrightarrow 0 \)

\( \Rightarrow \,\,\overrightarrow {NA}  + \overrightarrow {NI}  = \overrightarrow 0 \,\,\,\, \Rightarrow \,N\,\) là trung điểm của \(AI\).

LG b

Với các điểm \(M, N\) ở câu a) , tìm các số \(p\) và \(q\) sao cho

\(\overrightarrow {MN}  = p\overrightarrow {AB}  + q\overrightarrow {AC} .\)

Giải chi tiết:

Từ câu a), ta biểu diễn \(\overrightarrow {AM} ,\,\overrightarrow {AN} \) qua \(\overrightarrow {AB} ,\,\overrightarrow {AC} \).

\(\eqalign{
& \overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \,\, \Leftrightarrow \, - \overrightarrow {AM} - (\overrightarrow {AB} - \overrightarrow {AM} ) + (\overrightarrow {AC} - \overrightarrow {AM} )=\overrightarrow 0 \cr 
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \,\overrightarrow {AM} = - \overrightarrow {AB} + \overrightarrow {AC} \cr 
& 2\overrightarrow {NA} + \overrightarrow {NB} + \overrightarrow {NC} = \overrightarrow 0 \,\, \Leftrightarrow \, - 2\overrightarrow {AN} + \overrightarrow {AB} - \overrightarrow {AN} + \overrightarrow {AC} - \overrightarrow {AN} = \overrightarrow 0 \cr 
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \,4\overrightarrow {AN} = \overrightarrow {AB} + \overrightarrow {AC}\Leftrightarrow  \overrightarrow {AN}= {1 \over 4}(\overrightarrow {AB} + \overrightarrow {AC} ) \cr 
& \Rightarrow \,\,\overrightarrow {MN} = \overrightarrow {AN} - \overrightarrow {AM} = {1 \over 4}(\overrightarrow {AB} + \overrightarrow {AC} ) + \overrightarrow {AB} - \overrightarrow {AC} = {5 \over 4}\overrightarrow {AB} - {3 \over 4}\overrightarrow {AC} \cr} \)

Vậy \(p = {5 \over 4}\,;\,q =  - {3 \over 4}.\)