Bài 62 trang 137 SBT toán 6 tập 1

Đề bài

Lấy hai điểm \(I, B\) rồi lấy điểm \(C\) sao cho \(I\) là trung điểm của đoạn thẳng \(BC.\) Lấy điểm \(D\) sao cho \(B\) là trung điểm của đoạn thẳng \(ID.\) 

a) Có phải đoạn thẳng \(CD\) dài gấp ba đoạn thẳng \(IB\) không? Vì sao?

b) Vẽ trung điểm \(M\) và \(IB.\) Vì sao điểm \(M\) cũng là trung điểm của \(CD? \)

Lời giải chi tiết

Trên đường thẳng \(a\) lấy hai điểm \(I, B.\) Trên tia đối tia \(IB\) lấy điểm \(C\) sao cho \(IC = IB,\) trên tia đối tia \(BI\) lấy điểm \(D\) sao cho \(BD = BI.\) Ta có \(I\) là trung điểm của đoạn \(BC ;\) \(B\) là trung điểm của đoạn \(ID.\) 

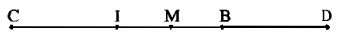
a) Ta có:

Vì \(I\) là trung điểm của đoạn \(CB\) nên \(\displaystyle IB = {{CB} \over 2}\) hay \(CB = 2IB\)

Vì \(B\) nằm giữa \(C\) và \(D\) nên \(CB  + BD = CD\)

Mà \(BD = IB\) (do \(B\) là trung điểm đoạn \(ID)\) nên \(CD = 2IB +IB \)\(= 3IB\)

Vậy \(CD=3IB.\)

b) Vì điểm \(M\) là trung điểm của đoạn \(IB\) nên \(\displaystyle MI = MB = {{IB} \over 2}\)

Ta có \(B\) nằm giữa \(I\) và \(D\) mà \(M\) nằm giữa \(I\) và \(B\) nên điểm \(B\) nằm giữa hai điểm \(M\) và \(D\). Do đó \(MD = MB + BD\) (1) 

Lại có \(I\) nằm giữa \(C\) và \(B\) mà \(M\) nằm giữa \(I\) và \(B\) nên điểm \(I\) nằm giữa hai điểm \(M\) và \(C\). Do đó \(MC = MI + IC.\) (2)

Từ (1) và (2) ta có \(MD = MB + BD\) và \(MC = MI + IC. \) Mà \(MI = MB;\)\( IC = BD\) nên \(MD=MI+IC= MC\)

Hay \(MD=MC\) (3)

Lại có \(M\) nằm giữa \(I \) và \(B\) nên \(M\) nằm giữa \(C\) và \(D. \) (4)

Từ (3) và (4) suy ra \(M\) là trung điểm của đoạn thẳng \(CD.\)