Bài 1.4, 1.5, 1.6 phần bài tập bổ sung trang 6 SBT toán 6 tập 2

Bài 1.4

Cho tập hợp \(\displaystyle M = \left\{ {2;3;4} \right\}\). Viết tập hợp \(P\) các số có tử và mẫu thuộc \(M\), trong đó tử khác mẫu.

Phương pháp giải:

Dựa vào định nghĩa : 

Người ta gọi \(\dfrac{a}{b}\) với \(a, b ∈ Z, b ≠ 0\) là một phân số, \(a\) là tử số (tử), \(b\) là mẫu số (mẫu) của phân số.

Giải chi tiết:

  \(\displaystyle P = \left\{ {{2 \over 3};{2 \over 4};{3 \over 2};{3 \over 4};{4 \over 2};{4 \over 3}} \right\}.\)

Bài 1.5

Tìm các cặp số tự nhiên \(n\) sao cho các phân số sau có giá trị là số nguyên :

\(\displaystyle{\rm{a}})\;{{n + 4} \over n}\)                                   \(\displaystyle b)\;{{n - 2} \over 4}\)

\(\displaystyle c)\;{6 \over {n - 1}}\)                                  \(\displaystyle{\rm{d}})\;{n \over {n - 2}}\)

Phương pháp giải:

Phân số \(\dfrac{a}{b}\) có giá trị là số nguyên khi tử số là bội của mẫu số, hay \(a = bk\) (với \(a, b, k \in Z; b\ne 0\)).

Giải chi tiết:

a) Ta có : \(\displaystyle \;{{n + 4} \over n} = \dfrac{n}{n} +\dfrac{4}{n}= 1+\dfrac{4}{n}.\)

Do đó, để phân số \(\displaystyle \;{{n + 4} \over n}\) có giá trị là số nguyên thì phân số \(\dfrac{4}{n}\) cũng phải có giá trị là số nguyên

\(\Rightarrow \) Số tự nhiên \(n\) là ước của \(4\) tức là \(\displaystyle n \in \left\{ {1;2;4} \right\}.\)

b) Phân số \(\displaystyle {{n - 2} \over 4}\) có giá trị là số nguyên khi  \(n – 2 \;⋮\; 4\)

    \(\Rightarrow  n-1 = 4k  \;(k ∈ N).\)

    \(\Rightarrow  n = 4k + 2 \;(k ∈ N).\)

c) Phân số \(\displaystyle {{6} \over n-1}\) có giá trị là số nguyên khi \(n – 1\) là ước của \(6.\)

  \(\Rightarrow \displaystyle n -1 \in \left\{ {-1;1 ; -2 ; 2;-3;3; -6;6} \right\}.\)

    Ta có bảng sau :

Vì \(n ∈ N\) nên \(\displaystyle n \in \left\{ {0;2;3;4;7} \right\}.\) 

d) Ta có : \(\displaystyle{n \over {n - 2}} = {{n - 2} \over {n - 2}} + {2 \over {n - 2}}\) \(= 1 + \dfrac{2}{n-2}\)

Do đó, để phân số \(\displaystyle \;{{n } \over n-2}\) có giá trị là số nguyên thì phân số \(\dfrac{2}{n-2}\) cũng phải có giá trị là số nguyên

\( \Rightarrow n - 2\) là ước của \(2\) hay \(n \in-2 \left\{ {-1; 1; -2; 2} \right\}.\)

Tó bảng sau :

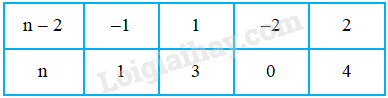
Vậy \(n \in \left\{ {0; 1; 3; 4} \right\}.\)

Bài 1.6

Cho \(\displaystyle{\rm{A}} = \left\{ { - 3;0;7} \right\}\). Hãy viết tất cả các phân số \(\displaystyle{a \over b}\) với \(a, b ∈ A.\)

Phương pháp giải:

Dựa vào định nghĩa : 

Người ta gọi \(\dfrac{a}{b}\) với \(a, b ∈ Z, b ≠ 0\) là một phân số, \(a\) là tử số (tử), \(b\) là mẫu số (mẫu) của phân số.

Giải chi tiết:

Số \(0\) không thể lấy làm mẫu của phân số.

Lấy \(-3\) làm mẫu, ta viết được \(3\) phân số là \(\displaystyle{{ - 3} \over { - 3}};{0 \over { - 3}};{7 \over { - 3}}.\)

Lấy \(7\) làm mẫu, ta viết được \(3\) phân số là \(\displaystyle{{ - 3} \over 7};{0 \over 7};{7 \over 7}.\)

Vậy ta viết tất cả được \(6\) phân số.