Luyện tập 4 trang 106 Tài liệu dạy – học Toán 8 tập 1

Đề bài

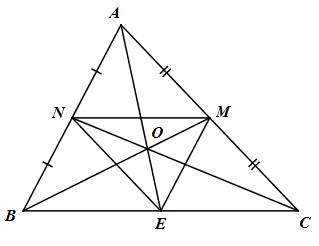
Cho tam giác ABC nhọn (AB < AC). Vẽ trung tuyến BM và CN.

a) Chứng minh rằng tứ giác BNMC là hình thang.

b) Gọi O là giao điểm của BM và CN. Tia AO cắt BC tại E. Tính chu vi tam giác ABC khi biết chu vi tam giác MNE bằng 12 cm.

Lời giải chi tiết

a) Xét tam giác ABC có:

M là trung điểm của AC (gt);

N là trung điểm của AB (gt);

=> MN là đường trung bình của tam giác ABC.

=> MN // BC => Tứ giác BNMC là hình thang.

b) ∆ABC có hai đường trung tuyến BM và CN cắt nhau tại O.

=> O là trọng tâm của tam giác ABC.

=> AE là đường trung tuyến của tam giác ABC => E là trung điểm của BC.

∆ABC có M là trung điểm của AC (gt) và E là trung điểm của BC (gt)

=> ME là đường trung bình của tam giác ABC \(ME = {1 \over 2}AB\)

∆ABC có:

N là trung điểm của AB (gt)

E là trung điểm của BC (gt)

=> NE là đường trung bình của tam giác ABC \(NE = {1 \over 2}AC\)

Ta có: \(NM + ME + NE = 12;NM = {1 \over 2}BC\) (NM là đường trung bình của tam giác ABC)

\(\eqalign{  & ME = {1 \over 2}AB;NE = {1 \over 2}AC \Rightarrow {1 \over 2}BC + {1 \over 2}AB + {1 \over 2}AC = 12  \cr  &  \Rightarrow {1 \over 2}(BC + AB + AC) = 12 \Leftrightarrow BC + AB + AC = 12.2 = 24(cm) \cr} \)

Vậy chu vi của tam giác ABC là 24 cm.

* Nhận xét: Đề bài toán thừa giả thiết tam giác ABC nhọn và AB < AC.