Giải Bài 9.17 trang 55 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
Tam giác ABC có AD, BE là hai đường phân giác và
Đề bài
Tam giác ABC có AD, BE là hai đường phân giác và \(\widehat {BAC} = {120^0}\). Chứng minh rằng DE là tia phân giác của góc ADC.
Phương pháp giải - Xem chi tiết
- Gọi Ax là tia đối của tia AB
-Chứng minh: \(\widehat {BAD} = \widehat {DAC} = \widehat {CAx}\)
- Hạ \(EH \bot Bx;EI \bot AD;EK \bot BC\)
-Áp dụng điểm nằm trên tia phân giác của góc thì cách đều 2 cạnh của của góc đó.
Lời giải chi tiết
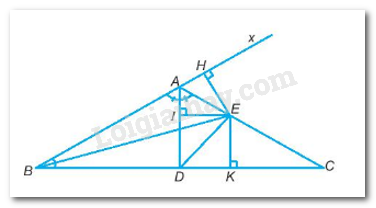
Gọi Ax là tia đối của tia AB \(\widehat {CAx} = {180^0} - \widehat {BAC} = {180^0} - {120^0} = {60^0}\) (2 góc kề bù)
AD là phân giác góc BAC
\( \Rightarrow \widehat {BAD} = \widehat {DAC} = \dfrac{{\widehat {BAC}}}{2} = \dfrac{{{{120}^0}}}{2} = {60^0}\)
\( \Rightarrow \widehat {BAD} = \widehat {DAC} = \widehat {CAx}\)
Hạ \(EH \bot Bx;EI \bot AD;EK \bot BC\)
Ta có:
EH = EK (vì BE là phân giác góc ABC)
EH = EI (vì AE là phân giác góc DAx)
\( \Rightarrow EK = EI\)
Vậy E nằm trên tia phân giác của góc ADC.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải Bài 9.17 trang 55 sách bài tập toán 7 - Kết nối tri thức với cuộc sống timdapan.com"







