Bài 2.1, 2.2, 2.3, 2.4, 2.5 trang 97, 98 SBT toán 6 tập 2
Giải bài 2.1, 2.2, 2.3, 2.4, 2.5 trang 97, 98 sách bài tập toán 6. Cho nửa mặt phẳng có bờ chứa là đường thẳng a và 3 điểm M, N, P (phân biệt). Nếu hai điểm M, N khác phía với đường thẳng a và hai điểm N, P ....
Bài II.1
Cho nửa mặt phẳng có bờ chứa là đường thẳng \(a\) và \(3\) điểm \(M, N, P\) (phân biệt). Nếu hai điểm \(M, N \) khác phía với đường thẳng \(a\) và hai điểm \(N, P\)
(A) khác phía với đường thẳng \(a\) thì hai điểm \(M, P\) khác phía với đường thẳng \(a;\)
(B) cùng phía với đường thẳng \(a\) thì hai điểm \(M, P\) cùng phía với đường thẳng \(a;\)
(C) cùng phía với đường thẳng \(a\) thì hai điểm \(M, P\) khác phía với đường thẳng a;\)
(D) cùng phía với đường thẳng \(a\) thì đôi một trong số các điểm \(M, P, N\) khác phía với đường thẳng \(a.\)
Phương pháp giải:
Vẽ hình theo các trường hợp của đề bài, từ đó chọn câu đúng trong các câu đã cho.
Giải chi tiết:
+) Khi hai điểm \(N, P\) khác phía với đường thẳng \(a\) ta có hình vẽ như sau :
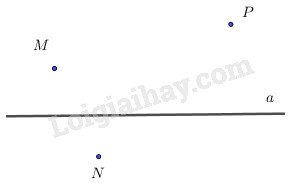
+) Khi hai điểm \(N, P\) cùng phía với đường thẳng \(a\) ta có hình vẽ như sau :
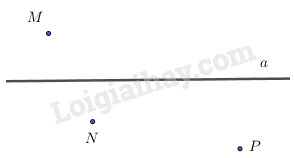
Vậy trong các câu đã cho, câu đúng là "Nếu hai điểm \(M, N \) khác phía với đường thẳng \(a\) và hai điểm \(N, P\) cùng phía với đường thẳng \(a\) thì hai điểm \(M, P\) khác phía với đường thẳng \(a.\)"
Chọn đáp án (C) Cùng phía với đường thẳng \(a\) thì hai điểm \(M, P\) khác phía với đường thẳng \(a.\)
Bài II.2
Số góc trong hình được tạo bởi \(6\) tia phân biệt, chung gốc bằng
(A) \(5; \) (B) \(6;\)
(C) \(15;\) (D) \(30.\)
Phương pháp giải:
Vẽ hình theo đề bài, từ đó đếm số góc tạo thành.
Giải chi tiết:
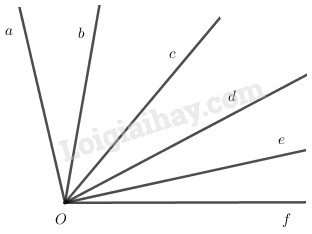
Đếm số góc được tạo bởi \(6\) tia phân biệt, chung gốc ta thấy có \(15\) góc khác nhau.
Chọn đáp án (C) \(15.\)
Bài II.3
Biết rằng \(\widehat {MNP} = 180^\circ \). Câu nào sau đây không đúng?
(A) Ba điểm \(M, N, P\) thẳng hàng;
(B) Hai tia \(MP\) và \(MN\) đối nhau;
(C) Hai tia \(NP\) và \(NM\) đối nhau;
(D) \(MNP\) là góc bẹt.
Phương pháp giải:
Vẽ hình theo đề bài đã cho, từ đó xác định tính đúng sai của các câu đã cho.
Giải chi tiết:
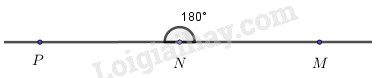
Trong các câu đã cho, câu không đúng là "Hai tia \(MP\) và \(MN\) đối nhau".
Chọn đáp án (B) Hai tia \(MP\) và \(MN\) đối nhau.
Bài II.4
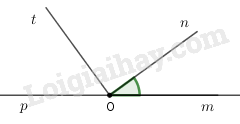
Vẽ \(\widehat {mOn} = 36^\circ \). Vẽ tiếp góc \(nOp\) kề bù với góc \(nOm\). Vẽ tiếp góc \(pOt\) phụ với góc \(mOn\) và tia \(Ot\) ở trong góc \(pOn\) (h.bs,6). Khi đó, số đo của góc \(nOt\) bằng bao nhiêu?
(A) \(54^\circ; \) (B) \(72^\circ;\)
(C) \(90^\circ;\) (D) \(144^\circ\)
Phương pháp giải:
Áp dụng các tính chất :
+ Hai góc kề bù là hai góc kề nhau và có tổng số đo bằng \(180^\circ.\)
+ Hai góc phụ nhau là hai góc có tổng số đo bằng \(90^\circ.\)
+ Nếu tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\) thì \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}\).
Giải chi tiết:
Vì góc \(nOp\) kề bù với góc \(nOm\) nên \(\widehat {mOn} + \widehat {nOp} =180^\circ\)
\(\Rightarrow \widehat {nOp} =180^\circ - \widehat {mOn}\) \(= 180^\circ - 36^\circ = 144^\circ.\)
Vì góc \(pOt\) phụ với góc \(mOn\) nên \(\widehat {mOn} + \widehat {pOt} =90^\circ\)
\(\Rightarrow \widehat {pOt} =90^\circ - \widehat {mOn}\) \(= 90^\circ - 36^\circ = 54^\circ.\)
Trên nửa mặt phẳng bờ chứa tia \(Op\) ta có \(\widehat {pOt} < \widehat {pOn}\) \((54^\circ < 144^\circ)\) nên tia \(Ot\) nằm giữa hai tia \(Op\) và \(On\)
\(\Rightarrow \widehat {pOt} + \widehat {nOt} = \widehat {pOn}\)
\(\Rightarrow \widehat {nOt} = \widehat {pOn} - \widehat {pOt}\) \(=144^\circ - 54^\circ = 90^\circ \)
Chọn đáp án (C) \(90^\circ.\)
Bài II.5
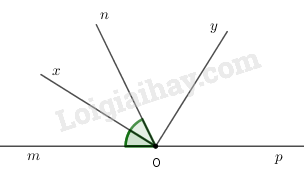
Vẽ \(\widehat {mOn} = 64^\circ \). Vẽ tiếp góc \(nOp\) kề bù với góc \(nOm\). Vẽ tiếp \(Ox\) là tia phân giác của góc \(mOn\). Vẽ tiếp \(Oy\) là tia phân giác của góc \(pOn\) (h.bs.7). Khi đó, số đo của góc \(xOy\) bằng bao nhiêu?
(A) \(90^\circ;\) (B) \(58^\circ;\)
(C) \(36^\circ;\) (D) \(116^\circ.\)
Phương pháp giải:
Áp dụng các tính chất :
+ Hai góc kề bù là hai góc kề nhau và có tổng số đo bằng \(180^\circ.\)
+ Nếu tia \(Oz\) là tia phân giác của góc \(xOy\) thì \(\widehat{xOz}=\widehat{yOz}=\dfrac{\widehat{xOy}}2\)
Giải chi tiết:
Vì góc \(nOp\) kề bù với góc \(nOm\) nên \(\widehat {mOn} + \widehat {nOp} =180^\circ\)
\(\Rightarrow \widehat {nOp} =180^\circ - \widehat {mOn}\) \(= 180^\circ - 64^\circ = 116^\circ.\)
Ta có \(Ox\) là tia phân giác của góc \(mOn\) nên \(\widehat{xOn}=\dfrac{\widehat{mOn}}{2} = \dfrac{64^\circ}{2} = 32^\circ\)
\(Oy\) là tia phân giác của góc \(pOn\) nên \(\widehat{nOy}=\dfrac{\widehat{pOn}}{2} = \dfrac{116^\circ}{2} = 58^\circ\)
Lại có \(On\) nằm giữa hai tia \(Ox\) và \(Oy\)
\(\Rightarrow \widehat {xOn} + \widehat {nOy} = \widehat {xOy}\)
\(\Rightarrow \widehat {xOy} = 32^\circ + 58^\circ = 90^\circ\)
Chọn đáp án (A) \(90^\circ.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 2.1, 2.2, 2.3, 2.4, 2.5 trang 97, 98 SBT toán 6 tập 2 timdapan.com"