Câu 61 trang 33 SGK Đại số 10 Nâng cao

Đề bài

Cho hai khoảng A = (m; m + 1) và B = (3; 5).

Tìm m để A ∪ B là một khoảng. Hãy xác định khoảng đó.

Lời giải chi tiết

A ∪ B là một khoảng khi A ∩ B ≠ Ø

Khi đó:

Ta thấy A ∩ B = Ø Khi m + 1 ≤ 3 hoặc m ≥ 5 tức là khi m ≤ 2 hoặc m ≥ 5.

Do đó A ∩ B ≠ Ø khi 2 < m < 5.

Hay A ∪ B là một khoảng ⇔ 2 < m < 5.

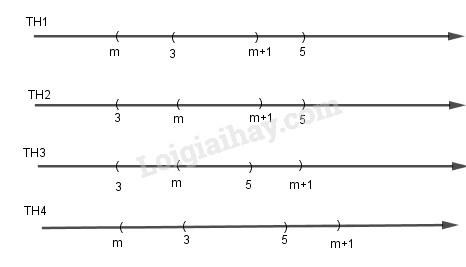
Ta xét các trường hợp:

TH1: \(m \le 3 < m + 1 \le 5\)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}m \le 3\\3 < m + 1\\m + 1 \le 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \le 3\\m > 2\\m \le 4\end{array} \right.\\ \Leftrightarrow 2 < m \le 3\end{array}\)

Khi đó \(\left( {m;m + 1} \right) \cup \left( {3;5} \right) = \left( {m;5} \right)\)

TH2: \(3 < m < m + 1 \le 5\)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}3 < m\\m + 1 \le 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 3\\m \le 4\end{array} \right.\\ \Leftrightarrow 3 < m \le 4\end{array}\)

Khi đó \(\left( {m;m + 1} \right) \cup \left( {3;5} \right) = \left( {3;5} \right)\)

TH3: \(3 < m \le 5 < m + 1\)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}3 < m\\m \le 5\\5 < m + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 3\\m \le 5\\m > 4\end{array} \right.\\ \Leftrightarrow 4 < m \le 5\end{array}\)

Khi đó \(\left( {m;m + 1} \right) \cup \left( {3;5} \right) = \left( {3;m + 1} \right)\)

TH4: \(m \le 3 < 5 \le m + 1\)

\( \Leftrightarrow \left\{ \begin{array}{l}m \le 3\\5 \le m + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \le 3\\m \ge 4\end{array} \right.\)

Không có giá trị nào thỏa mãn nên TH này không xảy ra.

Vậy:

+) Nếu 2< m ≤ 3 thì A ∪ B  = (m; 5)

+) Nếu 3< m ≤ 4 thì A ∪ B  = (3; 5)

+) Nếu 4< m ≤ 5 thì A ∪ B  = (3; m + 1)