Bài 4 trang 71 SGK Hình học 11
Giải bài 4 trang 71 SGK Hình học 11. Cho hình chóp S.ABCD
Đề bài
Cho hình chóp \(S.ABCD\). Gọi \(A_1\) là trung điểm của cạnh \(SA\) và \(A_2\) là trung điểm của đoạn \(AA_1\). Gọi \((α)\) và \((β)\) là hai mặt phẳng song song với mặt phẳng \((ABCD)\) và lần lượt đi qua \(A_1,A_2\). Mặt phẳng \((α)\) cắt các cạnh \(SB, SC, SD\) lần lượt tại \(B_1, C_1, D_1\). Mặt phẳng \((β)\) cắt các cạnh \(SB, SC, SD\) lần lượt tại \(B_2, C_2, D_2\). Chứng minh:
a) \(B_1, C_1, D_1\) lần lượt là trung điểm của các cạnh \(SB, SC, SD\).
b) \(B_1B_2 = B_2B\), \(C_1C_2 = C_2C\), \(D_1D_2 = D_2D\).
c) Chỉ ra các hình chóp cụt có một đáy là tứ giác \(ABCD\).
Phương pháp giải - Xem chi tiết
a) Sử dụng nội dung của định lí 2:
Cho đường thẳng a song song với mặt phẳng \(\alpha\). Nếu mặt phẳng \(\beta\) chứa a và cắt \(\alpha\) theo giao tuyến b thì b song song với a.
Và định lí đường trung bình của tam giác.
b) Sử dụng định lí đường trung bình của hình thang.
c) Dựa vào định nghĩa hình chóp cụt (SGK Hình học 11 trang 70).
Lời giải chi tiết
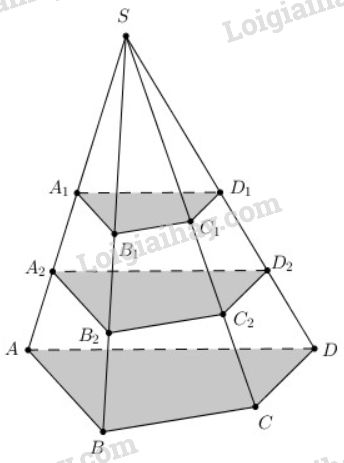
a) \((α) // (ABCD) ⇒ A_1 B_1 // AB\).
Mặt khác \(A_1\) là trung điểm của \(SA\) nên \(A_1B_1\) là đường trung bình của tam giác \(SAB\) \( ⇒B_1\) là trung điểm của \(SB\).
Chứng minh tương tự với các điểm còn lại.
b) Mặt phẳng \(\left( \beta \right)\) qua \({A_2}\) và song song \(\left( {ABCD} \right)\) \( \Rightarrow \left( \beta \right) \cap \left( {SAB} \right) = {A_2}{B_2}//AB\).
Mà \({A_2}\) là trung điểm của \(A{A_1}\) nên \({B_2}\) là trung điểm của \(B{B_1}\) hay \({A_2}{B_2}\) là đường trung bình của hình thang \(AB{B_1}{A_1}\). Do đó \({B_1}{B_2} = {B_2}B\).
Chứng minh tương tự ta được: \(C_1C_2 = C_2C\), \(D_1D_2 = D_2D\).
c) Có hai hình chóp cụt có một đáy là tứ giác \(ABCD\): \(ABCD.{A_1}{B_1}{C_1}{D_1};ABCD.{A_2}{B_2}{C_2}{D_2}\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 4 trang 71 SGK Hình học 11 timdapan.com"







